Nerf初入门笔记

推荐一个专栏, 转载自来源, 再加入自己的东西

#NeRF 是做什么的

通过使用稀疏的输入视图优化底层的的连续辐射体积场函数，实现复杂场景的新视角合成

#NeRF 是怎么做的

，(b)生成射线，(c)立体渲染，(d)算 mse loss。")

#Pipeline

nerf(二)---工作流程与基本原理

a).沿着相机光线的方向采样 5D 坐标
b).将坐标信息输入到 MLP 中，产生颜色和体积密度
c).使用立体渲染将颜色和体积密度合成为图像
d).渲染函数是可微分的，因此可以通过最小化合成图像和实际观察到的图像之间的残差来优化场景表示

#静态场景的表示

使用全连接（非卷积）深度网络(多层感知机，MLP)来表示场景
输入是一个连续的5D坐标：**空间位置 **$(x,y,z)$ 和 2D 观察方向$(\theta, \phi)$
输出是该空间位置的**体积密度 $\sigma$ 和视角相关的颜色 **$\textbf{c} = (r,g,b)$
这里的体积密度只对某一个空间点$(x,y,z)$ 而言，它表示一条穿过空间点$(x,y,z)$ 的射线累计了多少辐射(radiance)，后面会将它转化为概率密度

多视图之间保持连续一致性

体积密度 $\sigma$ 函数只与空间位置 $\mathbf{x}$ 有关 --> $\sigma(\mathbf{x})$
颜色 $c$ 函数与空间位置 $\mathbf{x}$ 和视角 $\mathbf{d}$ 都有关 --> $c(\mathbf{x},\mathbf{d})$

MLP 的设计

用 8 个全连接层来处理输入的空间坐标 $x$ (激活函数为 ReLU，每层256个通道)
输出 $\sigma$ 和一个 256 维的特征向量
将特征向量和视角方向 $d$ 连接起来
传递到一个额外的全连接层 (激活函数为 ReLU，128个通道)
输出依赖于视图的 RGB 颜色

MLP 的 Loss 计算
$\mathcal{L}=\sum_{\mathbf{r} \in \mathcal{R}}\left[\left|\hat{C}_c(\mathbf{r})-C(\mathbf{r})\right|_2^2+\left|\hat{C}_f(\mathbf{r})-C(\mathbf{r})\right|_2^2\right]$

用了两个 MLP 网络，分别是粗(coarse) 网络和细(fine) 网络

后续如何优化的部分会具体解释粗网络和细网络

$\mathcal{R}$ 是每个 batch 里面光线的集合，$\mathbf{r}$ 是指集合里面的每一条光线
$C(\mathbf{r})$，$\hat{C}_c(\mathbf{r})$，$\hat{C}_f(\mathbf{r})$ 分别是gt实景，粗网络，细网络中输出的光线 RGB 颜色
同时还将 $\hat{C}_c(\mathbf{r})$ 的损失最小化，以便粗网络的权重分布可以用于在细网络中分配样本

#神经渲染

https://zhuanlan.zhihu.com/p/486642042

沿着相机光线查询 5D 坐标来合成视图
使用立体渲染将输出颜色和密度投影到 2D 图像中

从特定的视角渲染 NeRF 的过程

利用穿过场景的相机光线，生成一组采样的三维点 $P_{3D}$
利用三维点和对应的 2D 视角方向作为 MLP 的输入，输出密度和颜色
使用立体渲染技术将输出颜色和密度累积到一个二维图像 $I_{2D}$ 中

由于具有可微性，所以可以利用梯度下降的方法来优化 MLP 网络，最小化每个观察图像和 NeRF 渲染出来的相应视图之间的误差

该部分详细内容参见 NeRF 的数学推导[NeRF数学公式从零推导](https://www.bilibili.com/video/BV1Wd4y1X7H1/)
光线可以表示为一个 3D 空间坐标
$\mathbf{r}(t) = \mathbf{o} + t \mathbf{d}$

原文中的一些假设：
场景是由一团发光粒子组成的，这里粒子密度的空间分布会发生变化
发射的光（每一个体素都会向四周均匀发出光）不随观察视角而改变

假设距离 $t$ 的近场边界和远场边界分别为 $t_n$ 和 $t_f$ ，那么对于一条射线，它的期望颜色表达式应该如下：
$C(\mathbf{r})=\int_{t_n}^{t_f} T(t) \sigma(\mathbf{r}(t)) \mathbf{c}(\mathbf{r}(t), \mathbf{d}) d t, \text{ where } T(t)=\exp \left(-\int_{t_n}^t \sigma(\mathbf{r}(s)) d s\right)$
函数 $T(t)$ 表示的是光线在 $t_n$ 到 $t$ 距离内的透射率，即光线在不碰到任何其他粒子的情况下能够传播的概率
一张示例图：

从连续的 NeRF 中渲染视图需要估计相机光线追踪的每个像素的积分 $C(\mathbf{r})$

这个很好理解，因为 2D 图像的每一个像素值实际上是相机发出的一条射线上的所有点累积叠加的结果

文中估计积分的方法是数值积分(Quadrature)
简单来说，就是分层抽样，把 $[t_n, t_f]$ 等分成 $\mathbf{N}$ 个区间，然后从每个区间内均匀随机地抽取一个样本

$t_i \sim \mathcal{U}\left[t_n+\frac{i-1}{N}\left(t_f-t_n\right), t_n+\frac{i}{N}\left(t_f-t_n\right)\right] \quad i =1,2,...N$

这里得到的 $t_i$ 是每个小区间内的随机抽取样本点的空间坐标

根据数值积分方法估计的颜色积分结果如下所示：
$\hat{C}(\mathbf{r})=\sum_{i=1}^N T_i\left(1-\exp \left(-\sigma_i \delta_i\right)\right) \mathbf{c}i, \text { where } T_i=\exp \left(-\sum{j=1}^{i-1} \sigma_j \delta_j\right)$
通过分层抽样的方式，将连续的积分变成了离散的求和，$\delta_i = t_{i+1} - t_i$ 是样本间隔(距离)
文中还提到了可以简化为传统的 Alpha 合成，对应的 alpha value 是
$\alpha_i = 1 - exp(-\sigma_i \delta_i)$

#如何优化

输入为一系列已知相机位姿的图像
两方面的优化：

使用位置编码来转换输入的 5D 坐标，将坐标映射到更高维度的空间中，使相似的内容分离到更远的地方，从而使 MLP 能够表示更高频率的函数，使得物体表面的几何和纹理更加逼真
采用了一种由粗到细的分层采样程序，对于颜色贡献大的点附近采样密集，贡献小的点附近采样稀疏，以减少必要的采样次数，充分采样整个高频场景表示

这个采样的过程应该是指相机光线对真实 3D 场景的采样，在输入到 MLP 之前

#位置编码(Positional encoding)

深度网络更偏向于学习低频函数，研究表明，在将输入通过高频函数映射到更高维空间后再传递给网络，可以更好地拟合包含高频变化的数据

将原先的表示函数变成两个函数的组合：
$F_{\Theta}=F_{\Theta}^{\prime} \circ \gamma$
两个函数，$F_{\Theta}^{\prime}$ 函数需要网络学习的，就是一个普通的 MLP，$\gamma$ 函数则不需要学习
$\gamma$ 在这里是一个映射(mapping) 函数，从空间 $\mathbf{R}$ 映射到高维空间 $\mathbf{R}^{2L}$
原文中使用的编码方程如下：
$\gamma(p)=\left(\sin \left(2^0 \pi p\right), \cos \left(2^0 \pi p\right), \cdots, \sin \left(2^{L-1} \pi p\right), \cos \left(2^{L-1} \pi p\right)\right)$
$\gamma(\cdot)$ 分别作用于空间坐标 $\mathbf{x}$ 中的每一个分量(x,y,z) 和视角方向的单位向量 $\mathbf{d}$ 的三个分量，最后会被归一化到区间 [-1, 1] 之间(sinh 函数)
文中用到的超参数

$L = 10 \quad \text{for} \quad \gamma(\mathbf{x})$
$L = 4 \quad \text{for} \quad \gamma(\mathbf{d})$

维度 $L$ 的选择和场景的复杂度以及算力有关，也决定了神经网络能学习到的最高频率的大小

#分层采样(Hierarchical volume sampling)

通过按照样本对最终渲染的预期影响进行比例分配提高渲染效率
同时优化两个 MLP 网络："coarse" 和 "fine"

将在相机射线上，由 near 和 far 构成的区间范围等分，然后在每个小区间内均匀采样得到一个采样点，一共 $N_c$ 个采样点
利用这些空间点来评估粗网络
再在每条射线上生成更多信息的采样点 (猜想是粗网络的结果输出了样本点的概率密度分布，为第二次采样提供了参考)
使用逆变换采样采样第二组 $N_f$ 个空间位置点，用两组空间点评估细网络，并使用两组空间点来计算射线最后的颜色 $\hat{C}_f(\mathbf{r})$

第三步具体是怎么做的
首先将原方程中粗网络 $\hat{C_c}(\mathbf{r})$ 的 Alpha 合成的颜色重写为沿着光线采样到的所有颜色 $c_i$ 的加权和
$\hat{C}c(\mathbf{r})=\sum{i=1}^{N_c} w_i c_i, \quad w_i=T_i\left(1-\exp \left(-\sigma_i \delta_i\right)\right)$

这个权值 $w_i$ 和透过率以及体积密度有关

将权值归一化后可以化为沿射线分布的分段常数概率密度函数(Piecewise-constant PDF), 目的是粗略估计射线上的物体分布情况
$\hat{w_i} = \frac{w_i}{\sum_{j=1}^{N_c}w_j}$

#细节说明

体积边界
对于合成图像: 缩放场景，使其位于以原点为中心、边长为 2 $([-1,1])$的立方体内，并仅查询这个边界体积内的 NeRF 表示
对于真实图像: 数据集包含可以存在于最近点和无穷远点之间的内容，用归一化的方式将这些点的深度范围映射到区间 [-1, 1]
这将所有光线的起点移动到场景的近平面(near plane)，将相机的透视光映射为变换后体积中的平行光线，并使用视差而不是使用度量深度，因此所有坐标都是有界限的
训练
对于真实场景的数据，在优化过程中对输出结果 $\sigma$ 添加了随机高斯噪声 (在通过 ReLU 之前)
渲染
在测试的时候，在每条射线上采样 64 个点输入到粗网络中，采样 64+128=192 个点到细网络中，每条光线一共采样 256 个点
对于合成的图片，每张图片需要 640k 条光线；对于真实场景，每张图片需要 762k 条光线

#NeRF 做的结果怎么样

#相关指标

PSNR: 峰值信噪比，是一种评价图像质量的指标 (越高越好)
SSIM: 结构相似性，是一种衡量两幅图像相似度的指标 (越高越好)
LPIPS: 学习感知图像块相似度，是一种度量两幅图像之间的差别的指标 (越低越好)

#优势

继承了体积表示的优点，可以表示复杂的几何形状和外观
适合使用投影图像进行基于梯度（可微）的优化
克服了在高分辨率建模复杂场景时，离散化体素网格所带来的存储成本过高的问题

#不足

训练速度太慢：每个像素都需要近 200 次 MLP 模型的前向预测
模型泛化性太差：NeRF 要针对每个场景单独进行训练，无法直接扩展到新出现的场景

#Nerf 不懂的地方

#Positional Encoding

思考Positional Encoding
map each input 5D coordinate into a higher dimensional space。
为什么要映射到高维空间：
This is consistent with recent work by Rahaman et al. [35], which shows that deep networks are biased towards learning lower frequency functions. They additionally show that** mapping the inputs to a higher dimensional space using high frequency functions** before passing them to the network enables better fitting of data that contains high frequency variation.

#3D occupancy fields

推荐博客: 1, 2
就是用一个隐函数来表示物体的连续边界.

体素表示的缺点：内存随分辨率呈立方增加，故需要限制在323232或646464。使用例如八叉树的数据自适应表示来降低内存，实现起来又会复杂，现有数据自适应算法依旧局限于相对较小的256256256分辨率。
点云表示的缺点：由于缺少底层网格的连接结构，需要额外的后处理来从模型中提取三维几何图形。
网格表示的缺点：现有的网格表示通常基于对一个模板网格的变形，因此不允许任意拓扑。

Occupancy Networks基于对连续三维占据函数进行直接学习的三维重建新方法。利用神经网络实现对任意分辨率的占据函数的预测。训练时大大降低了内存，推理时利用简单的多分辨率等值面提取算法从学习的模型中提取网格。

#a neural 3D texture field

a Texture Field as a mapping from 3D point p, shape embedding s and condition z to color c:

#light field sample interpolation techniques

远古方法了,不做了解,引用论文最迟都是2012年.

#Differentiable rasterizers

optimize mesh representations to reproduce a set of input images
可参考博客:1, 2

#alpha-compositing

Alpha合成（英語：alpha compositing）是一種將圖像與背景結合的過程，結合後可以產生部分透明或全透明的視覺效果。

#discretization artifacts

搞不懂,离散化伪影?
41 24 论文他们用的是什么方法

#view-dependent

view-dependent就是加入了direction（θ,ϕ），可以使得每个方向都有独立的颜色变化

#如何看图三

图三表示不同方向下，展示的结果会不一致，有镜面反射的效果
In the case of a fully Lambertian surface ( imagine an ideal “matte” surface like a terracotta vase), when a light ray hits a point the light enters slightly into the surface of the object and is scattered in all directions. In this case, I can look at the point from any direction and its color will be about the same. At the opposite extreme we have a perfect mirror: in this case each light ray is reflected in only one direction and this makes that, for example, when we look at a mirror what we see changes depending on where we are looking from. Fig. 3 of the paper shows the effect of the viewing direction

#inverse transform sampling

已知PDF和CDF后, 就可以求逆函数, 再通过采样均匀分布的点，将其代入到逆函数，进而得到服从指数分布的样本点(最终目标).
采样理论概述（逆变换采样、拒绝采样）

#DeepSDF

首先，我们可以用SDF（Signed Distance Function）这样一个函数来隐式地表示一个三维物体，输入是空间中点的三维坐标，输出是这个点离我们想表示的物体表面的最近距离，如果在外部就是正，内部就是负。显然只要SDF找的好，从理论上来说，我们就能够简单粗暴地表示任意复杂且连续的物体，这也是物体的隐式表示方式与用点云、体素、网格等表示方式相比最大的好处。

$S D F(\boldsymbol{x})=s: \boldsymbol{x} \in \mathbb{R}^{3}, s \in \mathbb{R}$
其中x为三维的采样点，s为一维的带正负的数值，假定真的有这样一个完美的SDF函数，那么我们就能用图形学中现成的Marching Cubes方法将其转换成网格数据，或者直接用raycasting方法直接渲染，在这里不作详细讨论。

现在假定我们有几个离散的SDF函数的输入与输出，我们想要通过某种方式得到这个完整的SDF函数，最终就能实现根据这几个离散的采样点来重建整个三维物体了，这也是本文的根本目的。本文提出的DeepSDF思想便是，用神经网络当做SDF函数的拟合器，训练完（或者说拟合完）之后，输入大量自定义的三维空间采样点，再提取出所有值为0的点组成面，就能够重建整个三维物体了。因为神经网络是万能函数拟合器，所以说这种方法可以表示任意精度的，连续的三维物体，只不过是得取决于你的采样点数量与神经网络的层数罢了
很显然，基于上面的思想我们很自然地想到这种结构：

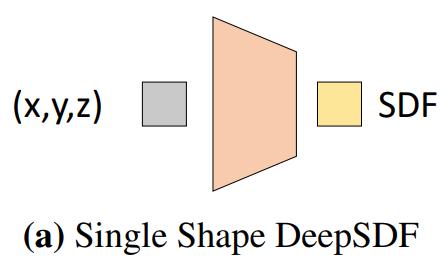
在这里，神经网络的作用不是去实现某种功能，而是去表示物体或场景本身，因此也会导致后续的各种训练上和我们正常认知的神经网络训练方式有些许的区别（关于这两者区别建议看一下《用神经网络表示物体或场景与用神经网络完成任务的区别与联系》）

这样就万事大吉了吗？并没有，因为如果用这种方法，并不是数据驱动的，而更像是一种数学的方法，我们每次进行重建的时候都得重新训练一个神经网络得到表示这个物体的专属SDF，比如给我一个轿车的若干采样点，我给训练出来了，你要是再给我一个卡车的采样点，我还得重新训练，虽说这样我们根本不需要数据集，但是缺点显而易见：我是希望在神经网络中引入对三维数据集的一些先验来辅助拟合，以便于更好地进行三维重建的，比如你就给我8个采样点，分别代表正方体的8个顶点，如果不引入数据集（如汽车数据集）的先验的话，最终拟合出来的东西肯定就是一个正方体（或者是个球体）之类的东西，而不是像个汽车的样子。
因此，本文提出了下面的架构：

假定数据集中的某类数据被编码成latent code进行表示，这样我将这个latent code和三维坐标同时丢入神经网络查询得到sdf值，其实就能够得到某类中某个具体的三维物体的SDF函数表示了

auto-coder