三维重建之路上

instant-ngp --scene data/nerf/fox 视频：计算机视觉之三维重建 找到一个同样是这个视频的笔记网址

#摄像机几何

#针孔模型 & 透镜

#针孔摄像机

物体直接映射到胶片上，会导致多个点映射到同一个点上，因此采用针孔成像。如下图，其中x,y,z是世界点Pw在摄像机坐标系上的坐标，已知；f是焦距，已知；由此可求得P'在像平面坐标。

#加透镜

可以让上述摄像机保持焦距越小，图像越清晰的情况下，增加亮度。 透镜将所有平行于光轴的光线汇聚到焦点，焦点到透镜中心的距离称为焦距（非上述焦距）。穿过透镜中心的光线的方向不会改变。 产生的问题：

• 失焦，物体“聚焦”有特定距离，一些地方清晰，一些地方模糊
• 径向畸变

#摄像机几何

为了将像平面图像（连续）转到数字图像（离散），使其可被建模。进行一些修正： 前三步是摄像机坐标系下

#偏置 单位变换

（下图f=f+z0,简化符号）

#转化为齐次坐标系

其中M是相机内参，不变矩阵，P是3D点，变化向量，建立了P'到P的线性关系

#插曲：将坐标转为线性关系

• 齐次坐标：EtoH：多加一维，值为1；HtoE：前n-1维除以第n维（E欧氏空间、H齐次空间）
• （α=fk。β=fl）
• 约定后续Ph写做P，除非特别指明是欧式空间下的P
• 

#摄像机偏移

工艺问题，不能垂直，所以需要加偏移系数 自由度：α，β，θ，Cx，Cy

#世界坐标系转换到摄像机坐标系

#摄像机模型P'=K[R T]Pw

RT矩阵具体内容不知道是什么，如有链接欢迎评论，后面的摄像机标定的补充知识有讲

#物理意义、自由度、欧式空间

1. 
2. 自由度：五个内参+6个外参（3个旋转3个平移）= 11个自由度（图中应该是1×4）
3. 齐次空间转换为欧式空间：

#Fauferas定理

零倾斜就是没有θ

#投影变换的性质

#其他摄像机模型

#规范化摄像机

#弱透视投影摄像机

当相对景深小于其与相机的距离时，可以对其进行一些简化，就简单地认为这些点就在一个深度上，直接投影到平面上，适合拍摄中远距离图像

• 其中f'为焦距，z0是物体到光圈O的距离，xy物体真实位置，x'y'像素面位置。这样子将z0固定为常数，使其为线性变换，而不是非线性变换。

v应该是 1×3 矩阵，Abv是K[R T]之后的结果

#正交投影摄像机

当摄像机中心到像平面距离无限远时，直接映射。

#总结

• 正交投影，更多地应用在建筑设计AUTOCAD，或者工业设计行业
• 弱透视投影在数学方面更简单，当物体较小且较远时准确，常用于图像识别任务
• 透视投影对于3D到2D映射的建模更为准确，用于运动恢复结构或SLAM
• 参考博客
  • 机器视觉学习（七）摄像机模型
  • 常用相机投影及畸变模型（针孔|广角|鱼眼）
  • 针孔相机成像模型
  • 二维坐标转换与坐标系转换
  • 三维空间中的几何变换-平移旋转缩放
  • 计算机图形学

#补充知识

#线性方程组的最小二乘解

#齐次线性方程组的最小二乘解

只需记住齐次线性用奇异值分解即可，后面经常用

#非线性方程组的最小二乘解

只需记住齐次非线性用牛顿、L-M方法即可，后面经常用

#摄像机标定

摄像机标定，即已知点坐标求解摄像机内、外参数矩阵，使得二维转三维可行。 更换符号：p=P'（像平面P'变为p） P=Pw（世界坐标Pw变为P）。

#标定问题基本思路

#超定齐次方程的原因

#转换成矩阵形式

#利用奇异值分解求超定齐次方程

其中M求解的值是真实世界的值差一个放大系数

#提取摄像机系数

详细过程参见：提取摄像机内参数 课堂知识：互相垂直点乘·为0（r1r2r3互相垂直）；r1×r2=r3 （另外图中矩阵大小可能有误）

#求u0、v0，放大系数ρ

不知道为什么a有时候转置有时候不转置 u0、v0就是偏置Cx、Cy r1·r3 = 0；r2·r3=0；r3·r3=1，且都互不相关，正交矩阵 （图中是点乘不是叉乘）

#求θ

然后左式子点乘 比上 右式子点乘即可出现下图 （具体看视频，虽然讲的也不怎么清楚，参考弹幕或前面的链接） ps. 如果θ=90° 则符合faugeras定理

#求α和β

如果α=β，则符合faugeras定理

#求外参r1，r2，r3

#求外参T

K满秩所必可逆

#总结

取点不能都位于同一平面，否则三点确定一个平面，多余的点都是没用的

#径向畸变的摄像机标定

#畸变模型

Sλ就是畸变矩阵

#非线性求解

m1m2m3是提取摄像机系数里的投影矩阵的三行

#求解线性部分加快迭代

ui÷vi即在原世界坐标下的等比例缩放直线，就那个d2

#补充知识

#2D平面上的变换

#欧式变换

#相似变换

#仿射变换

#透视变换

#3D变换

#欧式+相似变换

#仿射变换

#透视变换

#单视图几何

用单张图构建三维模型

#单视测量

00:17:46 影消点

#无穷远点、无穷远线、无穷远面

#2D空间

$url?imageMogr2/format/webp|?watermark/3/type/3/text/a2VlcGpvbGx5 用l表示一条直线 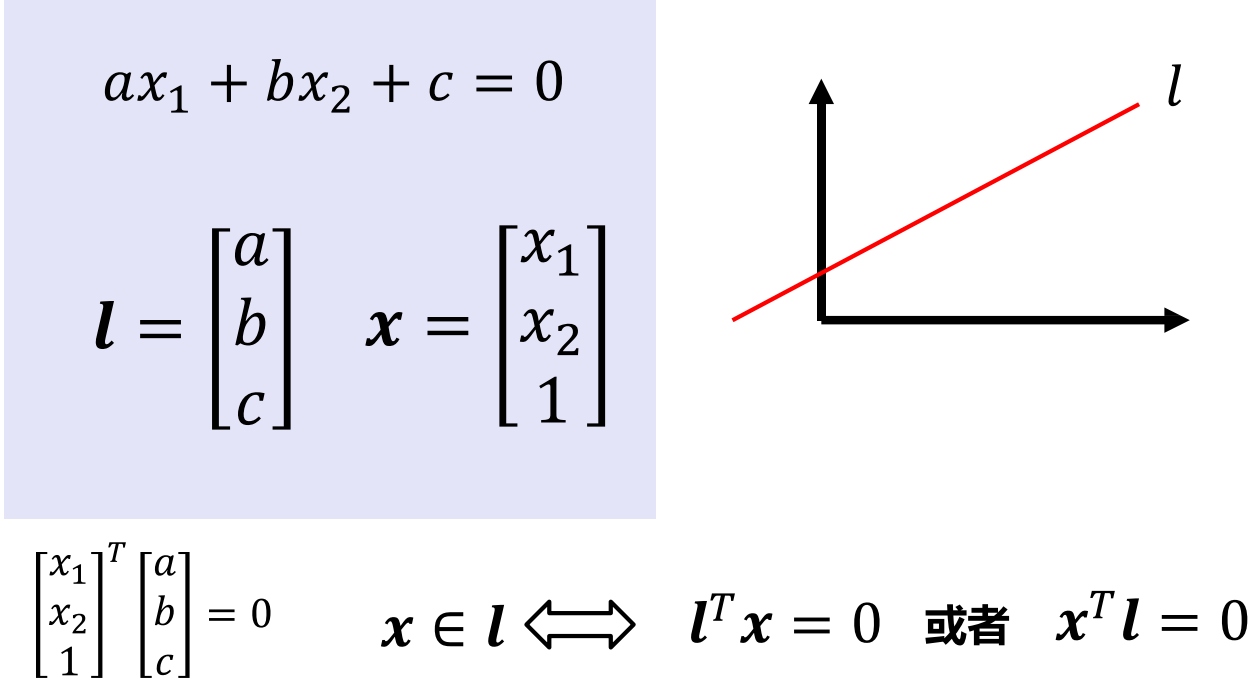x是两条直线的交点，x是l和l'的叉乘 2D空间中的无穷远点即当前直线方向的前两行加0即可。[a,b,0] 2D空间中的无穷远直线

#3D空间

• 3D空间的面

• 3D空间中的直线

为了方便，将其直线定义为直线方向，或者两平面的交线

• 3D空间中的无穷远点

根据2D中的无穷远点，即在直线方向上（a,b,c）最后一行多加0即可

• 3D空间中的无穷远平面

无穷远直线即为同个平面上的平行线上的无穷远点集汇聚成无穷远直线；或者是两个平行平面在无穷远处交与一条直线。视频位置33:30.

#影消点和影消面

#2D平面

• 无穷远点的变换

只要第三行为0就是无穷远点，透视除非v为0否则就不是。

• 无穷远线的变换

透视一般不是无穷远线，仿射一般是无穷远线。 因为仿射变换保持平行线不变，而透视变换可能会有在近处有交点而不会在无穷远处相交。

#影消点

影消点与直线方向 也可这样理解：K是做仿射变换，所以v=Kd（为什么这里证明的时候不考虑外参矩阵，摄像机坐标系？）

#影消线

• 橙色即影消线

#影消线与平面法向量

#总结（单视图重构关键）

#单视图重构

在假设下，θ已知，α=β，则还剩下Cx，Cy未知，一共三个变量未知？，并且v1v2v3互相在三维中是垂直关系，然后三个方程求解。

#总结

根据前面的求出摄像机内参矩阵后，就可以根据摄像机几何来获取像素点和三维点的关系，然后根据场景平面方向n来重建三维场景。 缺点是：场景的实际比例无法恢复，需要手动选择影消点与影消线，还需要场景先验信息（点对应关系，线、面几何信息等）

#总结

01:16:00.知道法向量和影消线的关系，影消点和直线的方向后，然后通过取三垂直的面来计算摄像机的内参矩阵，在两个假设下成立。然后通过法向量和影消线的关系，已知影消线就可求平面法向量，然后通过p=MP，获得三维点就可以三维重构了吗？期待评论单视图重构详细过程 推荐阅读博客：单视图测量

#Harris角点

视频地址

#uv与Euv的关系

通过观察uv的变化进而观察E(u, v)的变化，从而发现是不是角点，但是此处不方便，都需要经过I来计算，下面通过泰勒二阶展开，简化运算

#泰勒展开

得到M与Euv的关系，进而只需要分析M矩阵

#M矩阵对变化程度的关系

R是旋转矩阵使其变为水平椭圆， λ是方向变化剧烈程度，其值越大（λ1，λ2）则变化越快

#更进一步转化

#总结

• Partially invariant to affine intensity change
• Corner location is covariant w.r.t. translation
• Corner location is covariant w.r.t. rotation
• Corner location is not covariant to scaling!
  

#SIFT特征

#Scale selection

Spatial selection: the magnitude of the Laplacian response will achieve a maximum at the center of the blob, provided the scale of the Laplacian is “matched” to the scale of the blob
The response of a derivative of Gaussian filter to a perfect step **edge decreases as σ increases ** To keep response the same (scale-invariant), must **multiply Gaussian derivative by σ，**固定为1/√2Π Laplacian is the second Gaussian derivative, so it **must be multiplied by σ2 **

#Blob detection in 2D

前面听完一遍没听懂，可以去26:30min

#Characteristic scale 尺度特性

找到对应核后，就可以在图中画出对应圆圈，r=√2Πσ

#Scale-space blob detector

三个尺度为一组进行判断，只有尺度变化σ最大的那个点并且在333-1个点内是尺度变化σ最大的，才输出圆

#SIFT，更高效的做法

原先用拉普拉斯太耗时，图片越大计算量越大 下图听不懂的话继续往后听，在老师问大家的时候 回复3后面的时间讲的很清晰 1:09:20

1. 首先DoG近似于拉普拉斯算子，它利用差分来逼近，所以通过构造DoG减少运算量
2. 为了输出一个尺度空间，需要三个DoG结果，因此图中只能输出两个尺度空间k、k2（有可能会因为nms而减少，暂不考虑）
   1. 
   2. 同理：
      1. 这里因为下采样了，为了获得原图的圆半径大小，所以乘以2 [1:12:10]
3. 为了使其输出的尺度空间可以连续，即映射到坐标轴上是一条直线，从而根据σ推出半径r，进而比较最大值出现在那个尺度空间内，为了完成上述的Characteristic scale 尺度特性。
   1. 怎么连续呢，既让$k=2^{1/s}$(s是输出的尺度空间个数)，当s=2时，$k\sigma , k^2\sigma ,2k\sigma ,2k^2\sigma = \sqrt{ 2} \sigma,2\sigma,2\sqrt{ 2} \sigma,4 \sigma$,以√2倍的速率稳定增加，形成等比序列
4. 根据s可得DoG需要S+2层，高斯响应需要S+3层，然后计算各个k,k2,k3即可
5. 下采样的层是通过前一个采样层的倒数第三层得到，因为第三层（第3条.a小点）是$k^2\sigma = 2\sigma$，而下采样第一层是$\sigma$,相差两倍。
6. 有了下采样层就可以减少计算量了，因为像素点变少了

#真实应用的改进

#解决 affine covariance

利用M矩阵调整梯度大小，让小λ等于大λ ，使其$\lambda1\lambda2$一致，每次调整两个值的时候，同时修改检测圆的大小，

#解决角度问题

计算梯度方向直方图后，将其整体方向转到同一个方向，即可比较

#解决光照问题

将归一化后的图片计算各个局部格子的梯度方向直方图，为什么不用全局直方图是因为更细致一点，防止全局下虽然方向一致，但是局部其实不太一样。用4×4是因为精细程度适中，实验结果得出。

#匹配问题

近邻匹配

#识别&词袋模型

#视觉任务

#难点

• 类别多
• 视觉变换大
• 光照
• 尺度
• 形变
• 遮挡
• 物体和环境相似 background clutter
• 同个类别不同形状 intra-class variation
  

#基本问题

#Representation

• 用局部特征来表示一个物体
• 特征直接放到词袋内或者存储特征的相似关系
  • 
• 解决方法
  • 处理intra-class 变化，使用概率模型
  • 常用方法：产生式、判别式、混合式
    • 产生式是利用同个物体的特征相似度
    • 判别式是利用不同物体的特征差异性

#Learning

#Recognition

#How to represent an object category;

将图片表示成一个向量

#Bag-of-features models