二倍数对数组
思路就是 使得每一个奇数位置的值均是前一个位置的值的两倍，即凑成 n/2 对元素形如 (x, 2 * x) 的数对。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| # 利用python的Counter，计算每一个值的个数
# 只需要通过arr[2 * i + 1] = 2 * arr[2 * i] 是否符合即可
def canReorderDoubled(arr):
cnt = Counter(arr)
if cnt[0] % 2: # 如果0为奇数，则必不可能满足
return False
print(sorted(cnt, key=abs))
for i in sorted(cnt, key=abs):
if cnt[i] > cnt[2 * i]:
return False
cnt[2*i] -= cnt[i] # 将(小，大)中的大数删除，防止cnt[2*大]没有值
return True
# 用两个队列
# https://leetcode-cn.com/problems/array-of-doubled-pairs/solution/fen-jie-wei-liang-ge-dui-lie-by-mooc-3/
def canReorderDoubled(arr):
q1 = []
q2 = []
arr = sorted(arr)
for i in arr:
if i < 0:
if len(q1) and 2*i == q1[0]:
q1.pop(0)
else:
q1.append(i)
else:
if len(q2) and i == 2*q2[0]:
q2.pop(0)
else:
q2.append(i)
if not len(q1) and not len(q2):
return True
return False
|
寻找比目标字母大的最小字母
简单题重拳出击，二分法忘了😓
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| def nextGreatestLetter(self, letters, target):
for i in letters:
if ord(i)-ord(target) > 0:
return i
return letters[0]
# 二分
def nextGreatestLetter(letters, target):
n = len(letters)
l, r = 0, n - 1
while l < r:
print(l, r, l + r >> 1, (l + r) // 2, bin(l + r))
mid = l + r >> 1 # l + r >> 1 <=> (l + r) // 2 运算符优先级
if letters[mid] > target:
r = mid
else:
l = mid + 1
return letters[r] if letters[r] > target else letters[0]
# 一行
# https://leetcode-cn.com/problems/find-smallest-letter-greater-than-target/comments/1482439
def nextGreatestLetter(self, letters: List[str], target: str) -> str:
return letters[bisect.bisect(letters, target) % len(letters)]
|
区域和检索 - 数组可修改
前缀和概念：Link、Link2
int n = nums.length;
int[] preSum = new int[n + 1]; // 前缀和数组
preSum[0] = 0;
for (int i = 0; i < n; i++)
preSum[i + 1] = preSum[i] + nums[i];
先记住最精髓的一句话：树状数组本质是二进制规律的应用
假设现在有一个线性数组A,为了便于理解A的范围从1--8。
并构造一个数组C，范围也是1--8
接下来将C构造为那么一个树结构：
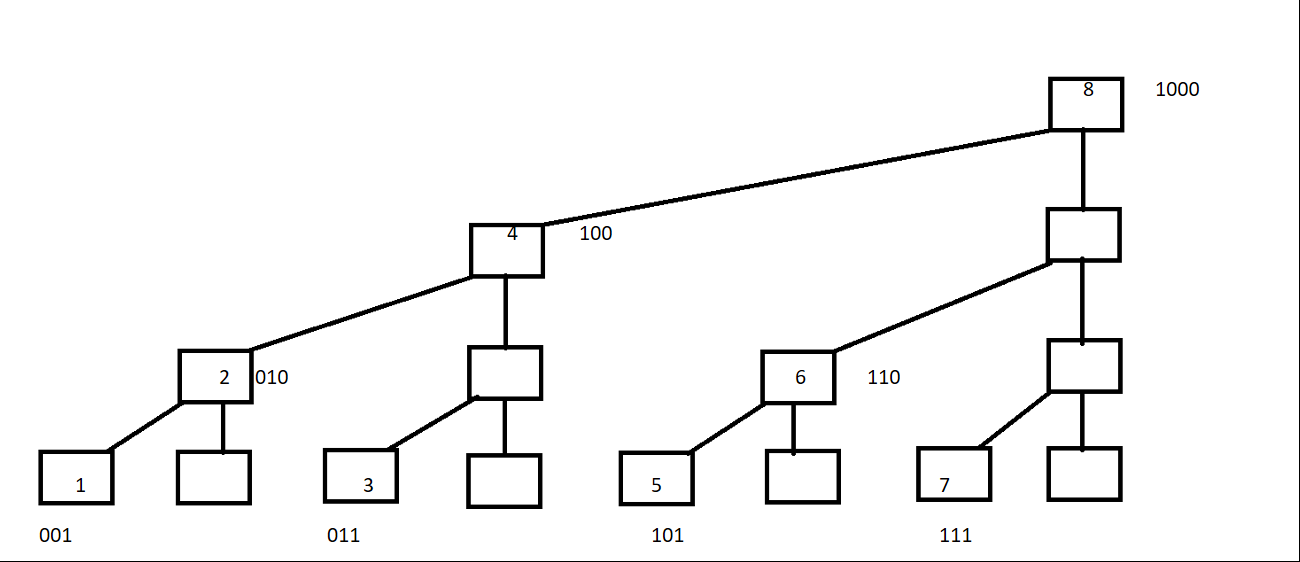
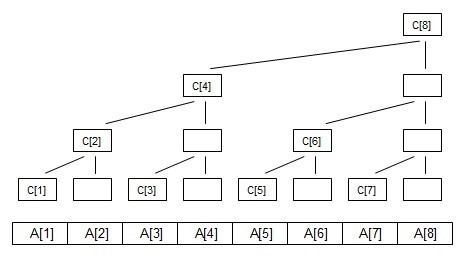观察这棵树结构，可以发现叶子结点的二进制的最后一位为1。接下来的结点为倒数第二位为1....
现在，我们对这棵树结构赋予其涵义：
二进制
1=(001) C[1]=A[1];
2=(010) C[2]=A[1]+A[2];
3=(011) C[3]=A[3];
4=(100) C[4]=A[1]+A[2]+A[3]+A[4];
5=(101) C[5]=A[5];
6=(110) C[6]=A[5]+A[6];
7=(111) C[7]=A[7];
8=(1000) C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];
这么说吧，这棵树的规律就是找出相应结点的二进制最后一位的1并该位后面的0也截出(后面会讲的lowBit函数)。
如5(101),最后一个1截出为1，那么它只有一个结点，那么他就是叶子结点。
如6(110),最后一个1截出为10，那么它这棵子树上有两个结点
非常重要：而某元素的父结点为该结点6(110)加上此结点的二进制截出最后一位的1(即010)(后面会讲的lowBit函数)。
如6(110)+2(010)=8(1000)
1.lowBit函数
1
2
3
| int lowBit(int x) {
return x & -x;
}
|
我们先需要知道lowBit函数的含义：可以用来获取某个二进制数的LowBit(即截出最后一个1及其后面的bit)
2.单点元素修改
结合上图：
当更新A[1]时(设新的A[1]比原来增加了d),需要自下向上更新C[1],C[2],C[4],C[8]
写为二进制：C[(001)],C[(010)],C[(100)],C[(1000)]
lowBit(1)=001 1+lowBit(1)=2(010) C[2]+=d
lowBit(2)=010 2+lowBit(2)=4(100) C[4]+=d
lowBit(4)=100 4+lowBit(4)=8(1000) C[8]+=d
总结规律：即找到1所在结点，然后用lowBit函数依次自下而上更新其所有父结点
3.求区间和
以求5-7之间的区间和为例，设区间和presum:
先求1-7之间的和，即7的前缀和。
7(111) presum+=C[7]
lowBit(7)=001 7-lowBit(7)=6(110) presum+=C[6]
lowBit(6)=010 6-lowBit(6)=4(100) presum+=C[4]
lowBit(4)=100 4-lowBit(4)=0(000)
总结规律：找到7所在结点，用lowBit函数不断消去最后一个1，并进行累加
再求1-5之间的和。
5(101) presum+=C[5]
lowBit(5)=001 5-lowBit(5)=4(100) presum+=C[4]
lowBit(4)=100 4-lowBit(4)=0(000)
最后将两个前缀和相减就得到区间和了。
python版代码在下面
作者：fenjue
链接：https://leetcode-cn.com/problems/range-sum-query-mutable/solution/by-fenjue-ewfb/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
| # 分块处理
class NumArray(object):
def __init__(self, nums):
n = len(nums)
size = int(n ** 0.5)
sums = [0] * ((n + size - 1) // size) # 向上取整，记住就好了
for i, num in enumerate(nums):
sums[i // size] += num
self.sums = sums
self.size = size
self.nums = nums
def update(self, index, val):
# 更新sums[块号]的值
self.sums[index // self.size] += val - self.nums[index]
self.nums[index] = val
def sumRange(self, left, right):
m = self.size
b1, b2 = left // m, right // m
if b1 == b2:
return sum(self.nums[left:right + 1])
# b1:[left: size-1] + sum(b2-b1) + b2: [0: right+1]
# b1的size-1 为前面块个数之和 即(b1+1)*m 因为块下标从0开始
# b2的b2*m 为前面块个数之和-1 即b2*m
return sum(self.nums[left: (b1 + 1) * m]) + \
sum(self.sums[b1 + 1: b2]) + sum(self.nums[b2 * m: right + 1])
obj = NumArray([1, 3, 5])
param_2 = obj.sumRange(0, 2)
print(param_2)
obj.update(1, 2)
param_2 = obj.sumRange(0, 2)
print(int(3 ** 0.5))
print(param_2, obj.nums)
# 树形数组
class NumArray(object):
# i += lowBit(i) 取出父节点
# i -= lowBit(i) 取出子节点
def __init__(self, nums):
self.A = nums
self.C = [0] * (len(nums) + 1)
self.n = len(self.A)
self.m = len(self.C)
for i in range(1, self.m):
self.C[i] += self.A[i - 1]
if i + self.lowbit(i) < self.m:
self.C[i + self.lowbit(i)] += self.C[i]
def update(self, index, val):
d = val - self.A[index]
# A的下标从0开始，C的下标从1开始，所以index+1
i = index+1
while i < self.m:
self.C[i] += d
i += self.lowbit(i)
# for i in range(index + 1, self.m): # 不能这样子写for
# self.C[i] += d
# i += self.lowbit(i)
self.A[index] = val
def sumRange(self, left, right):
l, r = 0, 0
i = right + 1
while i >= 1:
r += self.C[i]
i -= self.lowbit(i)
i = left
while i > 0:
l += self.C[i]
i -= self.lowbit(i)
return r - l
def lowbit(self, x):
return x & -x
|
针对不同的题目，我们有不同的方案可以选择（假设我们有一个数组）：
数组不变，求区间和：「前缀和」、「树状数组」、「线段树」
多次修改某个数（单点），求区间和：「树状数组」、「线段树」
多次修改某个区间，输出最终结果：「差分」
多次修改某个区间，求区间和：「线段树」、「树状数组」（看修改区间范围大小）
多次将某个区间变成同一个数，求区间和：「线段树」、「树状数组」（看修改区间范围大小）
总结一下，我们应该按这样的优先级进行考虑：
- 简单求区间和，用「前缀和」
- 多次将某个区间变成同一个数，用「线段树」
- 其他情况，用「树状数组」
作者：AC_OIer
链接：https://leetcode-cn.com/problems/range-sum-query-mutable/solution/guan-yu-ge-lei-qu-jian-he-wen-ti-ru-he-x-41hv/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。